A question for you surveyors
- Thread starter GrantMO
- Start date
- Views: 2248
patrickg
Veteran Member
Not a surveyor B U T ... Depends on how much lower you are willing to accept the center of the building with respect to "grade" when compared to the ends of the building. Or conversely, what depth (height?) of fill are you willing to put under the ends of the building? This isn't rocket science, just highschool math ( I was invited to drop algebra II the first time I took it and thrown out of class by the second teacher I took it from so what do I know about highschool math?).
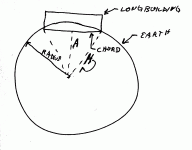
Re the terrific diagram... We see a large building with each end at grade and the center below grade. If the center were at grade then you would have to build up the pad at both ends to support the building. Same basic problem...
Anyway, we see that the radius of the earth is the hypotneuse of the right triangle with sides H, A, and 1/2 the chord. the difference in length between the radius and side A is the depth of the center of the building below grade. Using the Pythagorean theorem which states that the square of the length of the hypotneuse is equal to the sum of the squares of the other two sides. What do we do?
One way is to pick a depth below grade for the center of the buillding.
1. Subtract that depth from the radius of the earth and square this result.
2. Subtract this squared result from the square of the radius of the earth
3. Take the square root of the result obtained in step 2.
This is the depth below grade if I didn't mess up in the algebra again!
If this isn't confusing enough, just let me know, I can make it more so.
Patrick
Re the terrific diagram... We see a large building with each end at grade and the center below grade. If the center were at grade then you would have to build up the pad at both ends to support the building. Same basic problem...
Anyway, we see that the radius of the earth is the hypotneuse of the right triangle with sides H, A, and 1/2 the chord. the difference in length between the radius and side A is the depth of the center of the building below grade. Using the Pythagorean theorem which states that the square of the length of the hypotneuse is equal to the sum of the squares of the other two sides. What do we do?
One way is to pick a depth below grade for the center of the buillding.
1. Subtract that depth from the radius of the earth and square this result.
2. Subtract this squared result from the square of the radius of the earth
3. Take the square root of the result obtained in step 2.
This is the depth below grade if I didn't mess up in the algebra again!
If this isn't confusing enough, just let me know, I can make it more so.
Patrick
Attachments
Egon
Epic Contributor
Well; if'n you used some sky piles really wouldn't be any limit to the size. Guess you'd also have to use some sky hooks to hold up the pile driver. Don't know if the Hiely chelis [ sp ] formulas would apply though.
Egon
Egon
Anonymous Poster
Epic Contributor
- Joined
- Sep 27, 2005
- Messages
- 29,678
<font color=blue>...If this isn't confusing enough, just let me know...</font color=blue>
Hi Patrick...
How did I know...? /w3tcompact/icons/wink.gif
I just knew you'd come through... /w3tcompact/icons/smile.gif
Hi Patrick...
How did I know...? /w3tcompact/icons/wink.gif
I just knew you'd come through... /w3tcompact/icons/smile.gif
EdKing
Platinum Member
I just have to know, are you planning on a big building ?
Ed King
Ed King
Patrick,
I understood there would be no math. But seriously, consider you have an aircraft assembly line in a straight mile-long building on a flat piece of ground. If you run a laser at five feet above ground does it hit exactly five feet above ground a mile away? How about 10 miles? On the ocean, doesn't the horizon disappear at about 22-23 miles?
Ed,
Yes, and wait until you see the size tractor I store in such a building./w3tcompact/icons/wink.gif
I understood there would be no math. But seriously, consider you have an aircraft assembly line in a straight mile-long building on a flat piece of ground. If you run a laser at five feet above ground does it hit exactly five feet above ground a mile away? How about 10 miles? On the ocean, doesn't the horizon disappear at about 22-23 miles?
Ed,
Yes, and wait until you see the size tractor I store in such a building./w3tcompact/icons/wink.gif
EdKing
Platinum Member
Beter make it that wide to, so you have room to turn it around. /w3tcompact/icons/wink.gif
Ed King
Ed King
patrickg
Veteran Member
Grant, There is a brick building at Tinker AFB that is a mile long but it isn't an aircraft assembly line.
I was there a few times. Unfortunately I didn't have my laser with me, I wasn't even bright enough to think to sight down any mortar lines on the outside to see if I could see the curve.
Actually the horizon isn't any particular distance away at sea. It depends on your "Height of Eye" (distance of your eye above the water which on a typical day is changing with swell/waves depending on your boat. Thids variation due to waves/swell is negligible if it is a small percentage but matters if you are on a itsy bitsy boat. If you are overboard, say swimming, the horizon is not very far away at all. If you are on the bridge of a container ship the horizon is much farther away than from the cockpit of my last sailboat (lived aboard for almost 9 years).
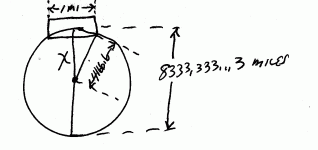
Ok lets do some "back of the envelope" rough estimation calculations.. Lets say it is 25000 miles around the earth and that it is a sphere. So pi (3) times the diameter is the distance around so 25000 miles/3 = 8333.333...3 miles Then the radius is 8333.333...3 miles/2 = 4166.666...6 miles
Refering to terrific drawing #2 (see attachment) we see the diameter of the earth, the radius, the hanger...
We have a right triangle composed of the radius of the earth, 1/2 the length of the hanger, and the distance from the floor to the center of the earth which is just a bit less than a radius. If we solve the right triangle for the just-a-bit-less-than-a radius side we can subtract that from the radius and have the vertical distance that the center of the floor would be below ground if the ends of the building were at grade and the earth were a perfect sphere 25000 miles around. X is the distance from the center of the earth to the bottom of the center of the building. So using the theorem of Pythagoras...
1. we square the radius and get 17361111.111...1 square miles.
2. we square the distance from the center of the building to the end 1/2 mile times 1/2 mile gives us 1/4 square miles
3. we subtract 1/4 from 17361111.11111111...1 and get 17361110.8611111111111111111111083
4. Taking the square root of 17361110.8611111111111111111111083 gives us 4166.66663666666655866666588906633
5. subtracting that from 4166.6666666666666666666666666666 gives us our answer 0.00003 miles
or converting to feet we get 0.158400000570240004105728 feet or 1.900800006842880049268736 inches
If one end of the building were at grade and the other straight out it would be 3.8 inches higher above grade.
NOTE: for better accuracy you could use pi as 3.14159265357989 or whatever it is instead of 3 like I did. You could use a better number for the size of the earth as well. Still, I don't think we exceed 10% error. I used the calculator supplied with Windoze 98. Hope it works better than much of the rest of this Gatesian nightmare.
Patrick (Not a surveyor but I hired one once)
I was there a few times. Unfortunately I didn't have my laser with me, I wasn't even bright enough to think to sight down any mortar lines on the outside to see if I could see the curve.
Actually the horizon isn't any particular distance away at sea. It depends on your "Height of Eye" (distance of your eye above the water which on a typical day is changing with swell/waves depending on your boat. Thids variation due to waves/swell is negligible if it is a small percentage but matters if you are on a itsy bitsy boat. If you are overboard, say swimming, the horizon is not very far away at all. If you are on the bridge of a container ship the horizon is much farther away than from the cockpit of my last sailboat (lived aboard for almost 9 years).
Ok lets do some "back of the envelope" rough estimation calculations.. Lets say it is 25000 miles around the earth and that it is a sphere. So pi (3) times the diameter is the distance around so 25000 miles/3 = 8333.333...3 miles Then the radius is 8333.333...3 miles/2 = 4166.666...6 miles
Refering to terrific drawing #2 (see attachment) we see the diameter of the earth, the radius, the hanger...
We have a right triangle composed of the radius of the earth, 1/2 the length of the hanger, and the distance from the floor to the center of the earth which is just a bit less than a radius. If we solve the right triangle for the just-a-bit-less-than-a radius side we can subtract that from the radius and have the vertical distance that the center of the floor would be below ground if the ends of the building were at grade and the earth were a perfect sphere 25000 miles around. X is the distance from the center of the earth to the bottom of the center of the building. So using the theorem of Pythagoras...
1. we square the radius and get 17361111.111...1 square miles.
2. we square the distance from the center of the building to the end 1/2 mile times 1/2 mile gives us 1/4 square miles
3. we subtract 1/4 from 17361111.11111111...1 and get 17361110.8611111111111111111111083
4. Taking the square root of 17361110.8611111111111111111111083 gives us 4166.66663666666655866666588906633
5. subtracting that from 4166.6666666666666666666666666666 gives us our answer 0.00003 miles
or converting to feet we get 0.158400000570240004105728 feet or 1.900800006842880049268736 inches
If one end of the building were at grade and the other straight out it would be 3.8 inches higher above grade.
NOTE: for better accuracy you could use pi as 3.14159265357989 or whatever it is instead of 3 like I did. You could use a better number for the size of the earth as well. Still, I don't think we exceed 10% error. I used the calculator supplied with Windoze 98. Hope it works better than much of the rest of this Gatesian nightmare.
Patrick (Not a surveyor but I hired one once)
patrickg
Veteran Member
Egon
Epic Contributor
Tried using a skyhook today but found it always fell down.
Then I thought about the question some more and considered the oblate speriod we live on and then started to think of a right angle to a radial line from the center of mass and came to the conclusion the size of the building would have to be approaching zero for the curvature to not have any effect.
Someones been pulling our chain!!!
Egon
Then I thought about the question some more and considered the oblate speriod we live on and then started to think of a right angle to a radial line from the center of mass and came to the conclusion the size of the building would have to be approaching zero for the curvature to not have any effect.
Someones been pulling our chain!!!
Egon
