While I'm very impressed with the construction of the indicator, after a little thought I've come to the conclusion that the math behind it isn't that complicated.
View attachment 495811
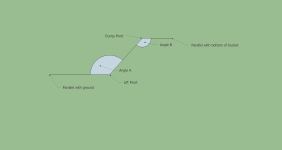
The drawing shows three lines: one that is parallel to the ground going through the lift pivot, one going between the lift pivot and the dump pivot, and one going through the dump pivot parallel with the bottom of the bucket. When Angle A equals Angle B, the bottom of the bucket is parallel with the ground. So what you need is a way of comparing Angle A with Angle B.
Measuring the angle of a pivot is straightforward: put an indicator pointer on the part that moves, and put a dial on the part that doesn't, and read the angle of the indicator on the dial. However, we want to compare Angle A with Angle B, and they're about six feet apart. How do we get the measurement from Angle B next to Angle A where we can read it? We could do that if we had someway of transmitting the movement back to Angle A. If you put an indicator needle on Angle B, and then connect it to a needle of exactly the same length through a rigid rod at Angle A, the indicator at A will move exactly the same amount as the indicator at B.
Then all you have to do is level the bucket and zero the two indicators.
The hard part isn't the geometry, it's the construction!