making an hydraulic thumb for my new mini-excavator

[dfkrug]

OK, now a few calculations for those who might wonder.

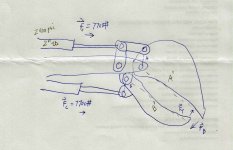
The goal here is to make a thumb that does not over-power the bucket, and vice versa. I have scribbled up a drawing to help illustrate my design.

Each cylinder is 2" (50mm) ID, and the pump puts out about 2400psi. This yields a pushing force of about 7700psi, maximum. The bucket cylinder pushes about the bkt pivot, with moment arm, A. The thumb pushes about the thumb pivot, with moment arm, B.

After sizing the cylinders (both 2" ID), the second major design parameter is to make A and B the same length. Unfortunately, the geometry of the thumb forced me to go with a somewhat larger B, in order for the thumb to swing fully out of the way. So, I ended up with A at 3.5", and B at 5". A' is the length of the bucket, from pivot to tip (15"), and B' is the length of the thumb, from pivot to tip (17").

The forces on the bkt or thumb vary widely, depending on the angle of the moment arm, and the pressure point of the load on the bkt and thumb. For simplification, I will look at the forces on the tips of each, when the moment arms are each at their positions where maximum forces are applied. These are the vectors, F(T) and F(B) in the drawing. The ratios of moment arm to element length are: A/A' = .23 for the bkt, and B/B' = .29 for the thumb. This means that the magnitude of F(T) = .29 x 7700 = 2270#. For the bucket, F(B) = .23 x 7700 = 1800#

The thumb can push harder than the bucket, but is that a problem?

If the thumb pushes on the bkt with 2270#, the resulting force on the bkt cylinder will be 2270/.23 = 9870#. 9870/piRsqd = 3140psi. Given the construction of these cylinders, I am comfortable with that pressure, without using a work-port relief valve or crossover RV.

 

[ovrszd]

Knowing me,,, always trying to get more from equipment,,, I wouldn't attempt this without a relief valve.

 

[downsizingnow48]

I appreciate the clear explanation of calculating the forces. Next time I am in Mendocino will work up the same numbers for my B21 bucket and DIY thumb. It will be interesting to see what is actually going on. Thanks.

 

[dfkrug]

On my backhoe thumb above, I was able to balance the thumb and bkt forces a little better by building the thumb from scratch and matching up the moment arm lengths somewhat closer. My thumb cylinder was low-end tierod type, customized. Definitely not as good as the welded cyls used on the mini-X.

Despite that, in over 200-300 hours of pretty hard use, I have not suffered any problems with over-pressure of one moving element over the other. Without any added RVs.

 

[Code54]

If it helps - on my Kubota Mini the thumb from the factory can be overpowered by the bucket. Not enough that it hurts anything but it works great.

 

[dfkrug]

If it helps - on my Kubota Mini the thumb from the factory can be overpowered by the bucket. Not enough that it hurts anything but it works great.

If you mean on your KX91, I suspect that the factory hydraulics are much more complicated than just another spool valve in the stack. Does it have the foot control that closes the thumb when you push on it, then fully retracts when you let go? I once operated a Takeuchi like that.

If you see the thumb push the bucket, or vice versa, there must be at least one work-port RV in there.

 

[Code54]

Yes sir - on mine the thumb is, well, thumb controlled with a. rocker on the top of the joystick. Super easy and it really works great - seems like a very natural place for it. When you release it stays in the position you left it in. Sort of handy when cleaning up brush and such. I really don't have a clue how the hydro is plumbed but will stay it works perfectly.

 

[dfkrug]

Yes sir - on mine the thumb is, well, thumb controlled with a. rocker on the top of the joystick. Super easy and it really works great - seems like a very natural place for it. When you release it stays in the position you left it in. Sort of handy when cleaning up brush and such. I really don't have a clue how the hydro is plumbed but will stay it works perfectly.

So, when you press the switch, the thumb closes. Is the rocker switch momentary, or does it change the function of one of your levers?

 

[Code54]

It is totally separate of everything else on the machine (Momentary). I sits top center of the right stick so when you are running the machine you just lift your thumb up off the stick and it is sort of right their at 12 o'clock. Press left to close right to open - very easy to get used to as it just seems like where you would expect it. I also like it that I can work the thumb while moving the machine with my foot pedal (can get a little tricky moving the machine, swinging the boom and closing the thumb at one time but im learning to do it all at once when needed)