Mysfyt
Platinum Member
Need to know the deflection of 2-1/2" round steel bar, 44" long supported on both ends with 1000 lbs load in center. The bar is hardened to 100 ksi.
I found an online calculator that seems to do what you want.
Deflection Calculation
Need to know the deflection of 2-1/2" round steel bar, 44" long supported on both ends with 1000 lbs load in center. The bar is hardened to 100 ksi.
How is the end of the bar supported? Into a rigid structure (concrete wall or similar), or supported from underneath? It will make a pretty significant difference in the result.
Also the yield strength of the material (100 ksi), won't make a noticeable difference in the deflection. It will, however, affect the load which the bar will carry and still be able to return to its original shape when unloaded.
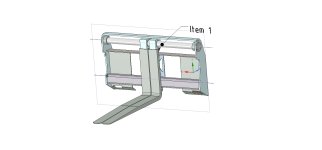
It needs to be a solid bar.2-1/2" round bar? That will be almost 60 lbs of steel... do you mean pipe? How about adding a center support and using 1 or 1-1/4 bar?
That's what I did when I built my forks. I've had all that my 3pt could carry on the forks (about 1800#) and nothing bent.2-1/2" round bar? That will be almost 60 lbs of steel... do you mean pipe? How about adding a center support and using 1 or 1-1/4 bar?
LD1 is correct, that bar is subjected to as much horizontal force as it is vertical, if not more. You also need to define the width of the center support, in this case the two fork brackets, as well as how the two ends are supported including the span of the end supports like jb1390 noted. It's much more complicated than a simple deflection calculation.
,,,,,,,,,,,,,,:thumbsup: ... [The amt of deflection the bar can withstand elastically.]How is the end of the bar supported? Into a rigid structure (concrete wall or similar), or supported from underneath? It will make a pretty significant difference in the result.
Also the yield strength of the material (100 ksi), won't make a noticeable difference in the deflection. It will, however, affect the load which the bar will carry and still be able to return to its original shape when unloaded.
To get the moment of inertia, its (pi x r^4)/4
to get deflection its (W x l^3)/(48EI)
Where:
W is weight in pounds
l is length in inches
E is modulus of elasticity. (steel is 30,000,000)
And I is the moment of inertia calculated in the first equation
So: The radius of 2.5" is 1.25. so (pi x 1.25^4)/4 = 1.917
(1000# x 44"^3)/(48 x 30,000,000 x 1.917) = 0.030" deflection