Superduty dump build

[powerstroke444e]

I put the correct numbers on your drawing hope that helps. All measurements down were from center of top pin

 

[LD1]

I put the correct numbers on your drawing hope that helps. All measurements down were from center of top pin

That helps a bunch. When I get a second, I'll calculate it.

But where did the 32" you mentioned come from. I see you changed that to 1'

It does make a little more sense now though. So the total be length is 10'6"??

 

[powerstroke444e]

32inch was about how far the 2 cylinder pins are apart IE Adjacent side of the triangle

 

[LD1]

Well, I got around to crunching some #'s

And it looks like you are going to have WAY more dump than you need:thumbsup: even @ 1500psi

If your measurments are accurate, the following is what I came up with:

The "effective" angle of the cylinder (due to the rear pivot placement as previously mentioned) is 20.2 degrees. The Sin of that is .345 In otherwords, you are using 34.5% of the cylinders force to dump the bed.

@ 2500psi, that is ~16,900 lbs of lift
@ 1500psi, that is ~ 10,150 lbs of lift

BUT, since the cylinder is mounted a good bit ahead of the center of the bed, that increases the mechanical advantage. By my calculations, its about a factor of 1.9:1

SO....

@ 2500psi, you have a lift force @ the center of ~32000lbs
@ 1500psi " " " " " ~19241lbs

That is not taking into effect any weight over that 6" of tail either that would reduce the effort needed to dump. :thumbsup:

And if the cylinder will extend to 90", you will have a dump angle of 45.2 degrees. Which should be more than enough to dump most things.:thumbsup:

And in an earlier post, you made a comment about liking to calculate these things, well....you are right. I enjoy doing this sort of thing. So thanks for sharing.

And I know you have already started building, but I'll throw you a link to the dump bed I built about a year and a half ago. It may give you some Ideas, or may not.

http://www.tractorbynet.com/forums/projects/158521-turning-1985-dodge-into-real.html

Keep us posted through the build

 

[Iplayfarmer]

That helps a bunch. When I get a second, I'll calculate it.

Let's see if you and I get the same numbers.

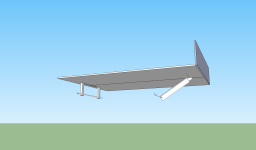
The final tilt of the bed is 44.2 degrees. This is based on the following assumptions...

-The ram is 32" pin center to pin center closed with a 58" stroke (90" pin to pin extended)
-The bed pivot hinge is 9 feet behind the top pin and 1 foot below the top pin.
-The bottom ram pin is 17" below the top pin.

And here are my only slightly less crappy drawings.

 

[Iplayfarmer]

...And if the cylinder will extend to 90", you will have a dump angle of 45.2 degrees. Which should be more than enough to dump most things.:thumbsup:...

Oh, look. You beat me to the calculation.

We're within a degree of each other. I guess that counts as a match.

I didn't run any force numbers, but I can agree that the force is plenty. Of course our "effective angles" are different as we are going about it from different directions.

I asked my neighbor who is a retired calculus teacher about the problem of finding the torque needed to dump a loaded bed. He couldn't offer any help. I can't believe that this is that rare of a problem.

 

[LD1]

Oh, look. You beat me to the calculation.

We're within a degree of each other. I guess that counts as a match.

I didn't run any force numbers, but I can agree that the force is plenty. Of course our "effective angles" are different as we are going about it from different directions.

I asked my neighbor who is a retired calculus teacher about the problem of finding the torque needed to dump a loaded bed. He couldn't offer any help. I can't believe that this is that rare of a problem.

The 32" pin center to pin center is where we are deviating a bit.

He said that his measurement was a rough one.

BUT using his #'s of 38" for retracted cylinder length AND the rear pin being 17" lower than the front, basic A2+B2=C2 for a right triangle puts that # @ 33.98" and that is what I used.

Try that and see if you come up with the 45.2 like I did.

PS, those are MUCH better drawings than mine. What program is that and does it calculat the angles for you as well??

I calculated it long-form using that "green" line I refered to earlier. The line drawn between the rear pivot and the RAM-BED pivot. Using the 9' and 12" numbers he gave us, that makes that "green" line 108.66" long. The cylinder is 38" long. Using the rest of his measurments I was able to determine that the distance between the rear pivot and the base cylinder pivot was 74.188" long.

Those three sides make a triangle. and using the cosine law (C2= A2 + B2 - 2ABcosC) the angle between the 108.66 and 74.188 sides was 10 degrees.

Since those two sides DONT change through out the dump, they remain constant. BUT the 38" side increases to 90". Using cosine law again, that makes THAT angle change to 55.2 degrees. Subtract the 10 degrees that it started with and it comes out to 45.2.

BUt I could have made an error in my calculations OR rounding, etc.

 

[Iplayfarmer]

The 32" pin center to pin center is where we are deviating a bit.

He said that his measurement was a rough one.

BUT using his #'s of 38" for retracted cylinder length AND the rear pin being 17" lower than the front, basic A2+B2=C2 for a right triangle puts that # @ 33.98" and that is what I used.

Try that and see if you come up with the 45.2 like I did.

PS, those are MUCH better drawings than mine. What program is that and does it calculat the angles for you as well??

I calculated it long-form using that "green" line I refered to earlier. The line drawn between the rear pivot and the RAM-BED pivot. Using the 9' and 12" numbers he gave us, that makes that "green" line 108.66" long. The cylinder is 38" long. Using the rest of his measurments I was able to determine that the distance between the rear pivot and the base cylinder pivot was 74.188" long.

Those three sides make a triangle. and using the cosine law (C2= A2 + B2 - 2ABcosC) the angle between the 108.66 and 74.188 sides was 10 degrees.

Since those two sides DONT change through out the dump, they remain constant. BUT the 38" side increases to 90". Using cosine law again, that makes THAT angle change to 55.2 degrees. Subtract the 10 degrees that it started with and it comes out to 45.2.

BUt I could have made an error in my calculations OR rounding, etc.

One of the reasons for the delay in my response was because I had originally figured the whole thing based on 38" pin to pin center. I went back and refigured after I saw powerstroke's response detailing 32" pin to pin measurement.

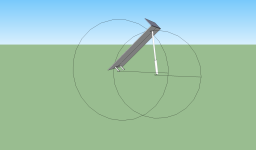
The program is sketchup. It's a free download. You'd like it, LD1. It will calculate the angles in that it will tell you how far you have rotated an object. I always figure the angle of motion in a situation like this by drawing two circles. One circle is centered on the ram base pin with a radius equal to the extended length of the ram. The other circle is centered on the articulation joint with a radius equal to the distance between the articulation point (dump joint in this case) and the ram rod end pin. (See attached picture.) Where the two circles meet is the extent of travel. When I move the bed in the picture to meet the extent of the travel I watch the indicator telling me how far I've rotated it.

Two very different methods came up with answers that are the same within the margin of error considering estimated numbers. That's good data.

One question about your calculations... The law of cosines only works on right triangles. There's no guarantee that the final triangle created between the bed length, extended ram, and the hinge to ram base is a right triangle. What am I missing?

 

[LD1]

One question about your calculations... The law of cosines only works on right triangles. There's no guarantee that the final triangle created between the bed length, extended ram, and the hinge to ram base is a right triangle. What am I missing?

You are missing that the law of cosines works on ANY triangle.

Its the pythagorean theorem that only works on right triangles.

And the pythagorean theorm is simply the law of cosines re-written.

The law of cosines (good for ANY triangle) is C2=A2 + B2 - 2AB(cosC)
and IF angle C is 90 degrees: the cosine of 90 is 0. So that completely cancels out the 2ABcosC and thus you are left with just C2=A2+B2

Law of cosines - Wikipedia, the free encyclopedia for a reference

 

[powerstroke444e]

I think next time I have a math problem I will pm one of you two:thumbsup:.

I figured I way over built this but wanted it heavy enought to put an a bigger truck down the road some day. One would guess that I wont have to worry about over loading the bed just the truck.

I ordered rest of the lights and picked up the wire to wire it. If all goes well should get it mostly done this weekend. Any good photo's of tailgates out there??? I think I have it figured out but just have build it.
LD1 you dump looks good would like to have that 4x4 when I am offroad as this thing needs a chain and tractor to get it to move offroad.

 

[Iplayfarmer]

... the cosine of 90 is 0. So that completely cancels out the 2ABcosC and thus you are left with just C2=A2+B2

That's the only part I remember from High School Trig. I use it all the time. Now that you've reminded the of the full thing, it might be even more useful.

 

[DumbDozer]

If the bed is 100" long for example, and the cylinder is hooked @ 50", the dump capacity would simply be the SIN of the angle mentioned above x the cylinder force. BUT if the cylinder is mounted farther forward of the rear pivot, like at 60", this increases the capacity by 6/5ths. And if farther back, it reduces capacity.

Egg-zactly, ( if I recall
close enuff for Govm't work,

under any circumstance, looks pretty dang neat to me!

 

[Iplayfarmer]

I finally figured it out!!! The equation to find the torque needed to begin dumping a bed is as follows...

(1/2 the length of the bed) X (weight of the load) = (initial torque needed)

I know this is the same thing that DumbDozer said, but I proved it to myself with multiple calculations, thought experiments, etc.

This equation assumes three things... The truck is level, the hinge is at the very back of the bed, and the load is evenly distributed. Any weight overhanging the back of the bed can be subtracted according to the same equation.

So, In PowerStroke's example with a 6500 pound load and a ten foot bed (ignoring the 6" overhang for now) the torque needed is 1/2 of 10' X 6500 lbs. = 32,500 ft.lbs. of torque. Where the ram is located 9' in front of the hinge, the vertical force needed at that point is 32,500/9 or about 3,611 pounds of vertical force.

To LD1's point, this is only the force in the direction of gravity. A few trigonometry calculations will get you the portion of that force that is tangent to the effective angle created by the hinge being lower than the top of the ram. I think I'm right. Correct me if I'm wrong.

 

[LD1]

That is actually very close to get a rough measurment.

In my previous example, using the 1500PSI numbers, I calculated that the cylinder force was ~10,000lbs and would dump almost 20,000lbs @ bed center.

Using your rough #'s:

A 20,000lb load would require 100,000ft-lbs of torque

100,000/9= ~11,000lbs of force required at the cylinder. Which is close to what I calculated.

This method you describe is good in the "design" stages of the build.

But doesn't help much to calculate the "actual" finished lift and angle specs.

For example, it will tell you how much force you NEED to have, but you still have to do a little trig to find out what the angle of the cylinder needs to be.

But as you have found out, there's more than one way to skin a cat:laughing:

 

[davygp38]

Good post, but what I am interested in doing, is to use a dump body with a gooseneck hitch. Could you post a picture of how you set it up?

 

[Iplayfarmer]

...But doesn't help much to calculate the "actual" finished lift and angle specs.

For example, it will tell you how much force you NEED to have, but you still have to do a little trig to find out what the angle of the cylinder needs to be.

But as you have found out, there's more than one way to skin a cat:laughing:

Understood. Keep in mind I've tackled the problem by calculating the force needed then one can calculate the force available. this series of formulas could even be used to determine the angle that the ram has to be placed at in order to generate enough lift to dump a bed. If someone is using a ram that is just barely big enough, the angle calculation may be very important.

The other thing that has to be considered is that these numbers generate baseline estimates. If a dump bed is loaded front heavy it will take more torque to dump it. If the truck is nose down that can also have an effect.

 

[powerstroke444e]

Did a little more work on the truck and I know the rule on the site is more pictures the better.

I got the tailgate built and built the rear of the bed IE were the tailgate contects. Made a 2way gate and will put a small grain door in it for the pea gravel will be easier to unload in to my small dump trailer that I pull with the atv with out spilling it.

Also built 2 toolboxes on the rear and with the other side boxes I have on top of these will be nice place to keeps chains straps or more junk

I will still have a 6 x 10 bed for material which with pea gravel dirt or sand it will be easy to over load.

 

[powerstroke444e]

Well got it painted today:thumbsup:. Here is a picture. I started wiring it and should have it done within the week.

 

[powerstroke444e]

Finally got it finished and took it out for the 1st time tonight all went well. Got all the lights working and strobes working. I have not had time to weigh it yet but later in the week going to haul a load of scrap so will know then. Yes stuff in tool boxes slide to back.
I put lights in all the boxes on the rear and in bed so I can see @ night they are a big help.

 

[Iplayfarmer]

The lights in the boxes sound like a great idea. The build looks good.