patrick_g said:
Folks just kept on focusing on friction, due to familiarity I suppose.
Pat,
You might be referring to me so I will argue that the major part of the equation is friction. Without friction the MCB cannot prevent the movement of the plane.
Tom_Veatch said:
I've been tempted to calculate the conveyor acceleration necessary to hold an airplane static relative to the tree sitter. But, so far, have successfully resisted that temptation.
Tom,
Well I wish you would have,

but since you didn't here goes...
In my previous posts I showed how an airplane could be made to takeoff from the MCB. I still think this is possible, however after the following calculations it becomes apparent that a few more modifications would be necessary...
First I will redefine the question for clarity.
If an airplane were placed on a large conveyor belt of sufficient size to support its weight, could the conveyor prevent forward motion of the airplane if:
The conveyor is capable of accelerating in excess of 5000m/s^2
The conveyor surface experiences no deformation (its flat).
The conveyor surface is comparable to dry asphalt in its friction coefficient.
The airplane is a standard production aircraft with standard equipment and rubber tires.
The conveyor is fixed to the earth at sea level.
The earth is the reference point. All motion will be regarded in reference to fixed points on the earth.
The airplane will be placed upon the conveyor with its main landing gear (wheels) centered on the midpoint of the conveyor belt.
The airplane will use thrust and brakes such that there is no sliding of the tires prior to brake release. Note: During this static runup there will be some movement of the aircraft as forces stabilize. Once in equilibrium this will be the referenced starting point.
Since I used the numbers for a U-2R in my previous posts I will continue here.
The calculations presented will use simple physics and mechanics formulas witch will give an approximation of values sufficient to gain an understanding of the magnitude of the forces involved. Finite element analysis and further computational analysis is left to the reader.
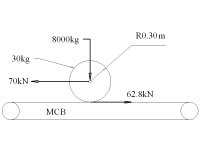
A/C weight = 8000 kg
Weight on each wheel = 2666.7 kg (assumed to be equal for all three wheels for simplification)
Normal force per wheel assembly = 20928 N
Wheel and tire weight = 50 kg
Wheel and tire diameter = 0.6 m
A/C thrust = 70 kN
Coefficient for rubber on asphalt = mu=0.8
Moment of inertia for the wheel and tire = I = 1/2mr^2 = 2.2 kgm^2
Force of static friction that the conveyor can exert on each tire = F = mN = 20.9 kN
Circumference of the wheels and tires = 2*pi*r = 1.885 m
Torque exerted on the tires by the conveyor = t = rFsin 90 = 6278.4 Nm
Angular acceleration = Aa = t/I = 2790.4 rad/s^2
Rotational acceleration = ARotational = Aa/2*pi = 444.1 revolutions/s^2
Conveyor acceleration = Ac = C*ARotational = 837 m/s2
This value represents the maximum linear acceleration of the conveyor to maintain a static contact with the wheel. Any faster and slippage occurs, any slower and its full potential in not utilized.
Velocity of the belt vs. time = VB =tAc
Centripetal Force (similar to the force on a string exerted by an object tied to that string and spun around in a circle) = FC = mv^2/r
Let’s assume 10 gram portions of the wheel and tire. So if the tire weighs 10 kg that breaks it up to 1,000 pieces for each tire and 4,000 pieces for each wheel with the following forces exerted over time. In reality (with actual testing) you would probably find that much larger portions of the tire/wheel assembly would be more realistic for calculation, yielding much larger forces.
Therefore we have the relationship between time in seconds, belt speed in m/s and mph, and Centripetal Force in Newtons and lbs
1 second, 837 m/s = 1872 mph, 23352 N = 5250 lbs
4 seconds, 3348 m/s = 7489 mph, 373636 N = 47250 lbs
7 seconds, 5859 m/s = 13106 mph, 1144236 N = 257253 lbs
10 seconds, 8370 m/s = 18723 mph, 2335230 N = 525006 lbs
This shows that there would be tire failure within a few seconds. At that point, depending on how catastrophic the failure, the wheels would drop to the conveyor and continue to accelerate at a slower rate (remember its all dependent on friction – steel wheels less friction slower acceleration of the conveyor).
So what about the airplane’s motion during these few seconds? Granted there is conservation of energy (transferred to the wheels) However there is a Net external force FNet External of 7216 N (see attached diagram). That gives us a net acceleration of 0.902 m/s2.
Velocity after 5 seconds = 4.5 m/s = 10.1 mph
Distance after 5 seconds = 11.2m
Velocity after 10 seconds = 9.2 m/s = 20.6 mph
Distance after 10 seconds = 45 m
The plane disintegrates before any appreciable lift is achieved, HOWEVER, there is forward motion.
Now if anyone is still with me at this point (and you thought Tom and Pat were long winded



), here is how a plane could take off from this conveyor. The limitation of the airplane would have to be removed. Then you simply replace the tires and wheels with something with a very small coefficient of friction, small radius and large mass. Two rollers (something like giant steel rolling pins) would keep the acceleration of the conveyor belt very low and the Net external force very high. The airplane would accelerate and fly. The calculations are left to you to prove me wrong.
Pardon me, while I go split some wood… with my TRACTOR.