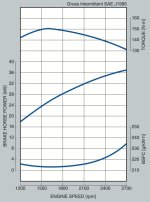
Okay, who wants a trip back to high school physics? Here's a problem for you to solve: How fast can a 4400 lb (2000 kg) tractor go up a 30 degree incline powered by an engine with performance shown in the attached graph? The graph is for a an actual Kubota engine that produces 50 hp (@2700 RPM) and 110 lb-ft of torque (@1600 RPM). Let's assume the tractor has a 12 speed, geared transmission that can cover the range of 1-12 mph, and it is lossless. Let's also assume that road friction is negligible. I recommend you use metric units for the calculation, and then convert the answer to mph at the end. (It's much, much easier that way.) To save you some time looking for your old text books, here are some hints: 1. The work performed is equal to m * g * h, where m is the mass of the tractor, g is the acceleration due to gravity (9.8 m/s), and h is the vertical height the mass is lifted. Work is measured in joules (J). 2. Power (P) is the rate at which work is performed. It is measured in W (watts), which is the same as J/s (joules per second). P = (m * g * h) / t, where t is time. 3. For a 30 degree incline, the distance traveled is double the height the mass is lifted. and some conversion factors: 1 m/s = 2.24 mph (velocity) 1 HP = 746 W (power) 1 kg = 2.2 lb (mass) 1 N-m = .74 lb-ft (torque) It shouldn't take more than a few minutes to come up with the answer. Cheers