LD1
Epic Contributor
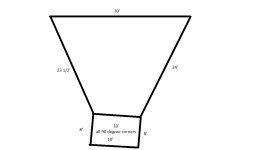
Cannot be solved. Need another piece of info. Either the overall height of the trapezoid, Distance between parallels.....that is assuming they are parallel (another assumption), One of the angles, etc.
Assuming they are parallel, simply adding an angle makes it solvable:
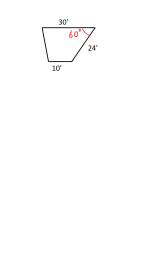
Sin60=h/24 will give us the height of the trapezoid. which would be 20.78.
then you can either use the trapezoid formula [(base + top) / 2 ] x height.......(10+30)/2 = 20.......20*20.78 = 415.xx
Or you can break it into right triangles. cos60=x/24 would give the third leg to the triangle on the right. Which would be 12.
So knowing the height, you now know everything needed.

Assuming they are parallel, simply adding an angle makes it solvable:
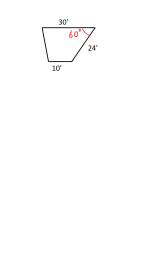
Sin60=h/24 will give us the height of the trapezoid. which would be 20.78.
then you can either use the trapezoid formula [(base + top) / 2 ] x height.......(10+30)/2 = 20.......20*20.78 = 415.xx
Or you can break it into right triangles. cos60=x/24 would give the third leg to the triangle on the right. Which would be 12.
So knowing the height, you now know everything needed.