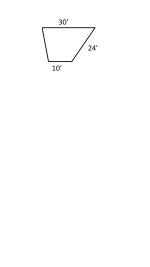You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Need help with my geometry
- Thread starter tallyho8
- Start date
- Views: 16427
More options
Who Replied?
/ Need help with my geometry
#41
Egon
Epic Contributor
[video]http://www.mathsisfun.com/area.html[/video]
Lnk
Gold Member
- Joined
- Feb 24, 2014
- Messages
- 368
- Location
- E TN
- Tractor
- Ferguson to-20, Deutz D7007, Yazoo yhr-60, Gravely 5240, Gravely C8 and model L,
It's been so long since I got out of school, I can't remember how to solve this problem.
I can't even remember if its geometry, trigonometry or whatever. Maybe its early Alzheimer's?
Please help me find out how many square feet this is.
View attachment 465525
436.348 Sq Ft.
smstonypoint
Super Member
- Joined
- Oct 13, 2009
- Messages
- 6,119
- Location
- SC (Upstate) & NC (Piedmont)
- Tractor
- NH TN 55, Kubota B2320 & RTV 900, Bad Boy Outlaw ZTR
436.3484845854290 square feet.
Steve
Steve
teejk
Veteran Member
- Joined
- Mar 3, 2012
- Messages
- 1,791
- Location
- Merrillan, WI
- Tractor
- JD 2020, IH CC 1250, Ariens 926 Snowthrower
Now somebody posted something above that jogged my memory. Put a triangle on both sides to form a rectangle. A) Calculate the area of that rectangle (even I remember that part). B)Then calculate the area of the triangles (a little fuzzy there but it is available quickly on-line). Subtract B) from A).
dieselcrawler
Elite Member
Due to the dimensions given, the length of the center rectangle was unknown. Sides A and C were known, so C Squared minus A squared equals B squared, in this case about 21.8 feet. Then it's easy...
westcliffe01
Veteran Member
The main dimension that needs to be calculated is the width between the 10ft and the 30ft sides. One has to assume that the figure is symmetrical, else one needs at least 1 more dimension.. It is also assumed that the 10ft and 30ft sides are parallel.
Using Pythagoras, the distance is (24^2-10^2)^.5 = 21.817ft
Now you can slice off the triangle on the right and add it to the diagram on the left to make a rectangle. The rectangle is now 20ft x 21.817ft. That yields a surface area of 436.348 sq ft.
Using Pythagoras, the distance is (24^2-10^2)^.5 = 21.817ft
Now you can slice off the triangle on the right and add it to the diagram on the left to make a rectangle. The rectangle is now 20ft x 21.817ft. That yields a surface area of 436.348 sq ft.
Redneck in training
Elite Member
Assuming the figure is symmetrical and the top and bottom lines are parallel. The height of the figure is calculated as (24^2 -10^2)^0.5 = (576-100)^0.5=21.81742'.
Then the area is 30*21.81742'=436.3485 as determined in several previous entries.
Then the area is 30*21.81742'=436.3485 as determined in several previous entries.
LD1
Epic Contributor
Yet another way to solve it. Now it is all Pathagorean.View attachment 465621
That is how I solved it. And get the 436.xxx as well.
But that is making the ASSUMPTION that the other diagonal leg is ALSO 24'. That wasnt a given as per the first drawing. As it stands, how the drawing is sketched up with current dimensions, and not knowing that it is symmetrical.....it is technically impossible to figure without some other numbers. Either angles, or length of the other diagonal.
Gathering more facts and knowing it is for a driveway apron.....I hope we can assume it will be symmetrical. Thus the conclusion of 436.xxx sq ft.
But its usually not good to automatically assume things in problems like this.
Exaggerated example, but solve this: