OP
CDN Farm Boy
Veteran Member
Thanks Aaron, that would be an option I hadn't considered.
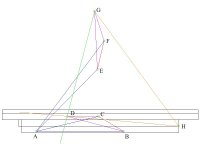
Spent the afternoon looking at scissor designs and playing with CAD and came up with the following. Please feel free to poke holes in it. This would reuse my existing 4x30 cyl and the existing lower cyl mount.
Point Legend:
A - Existing cyl base mount & scissor base mount
B - Scissor hinge pivot (lowered position)
C - Cyl/scissor mount (lowered position)
D - Scissor/bed mount (lowered position)
E - Scissor hinge pivot (raised position)
F - Cyl/scissor mount (raised position)
G - Scissor/bed mount (raised position)
H - Bed hinge
When the cyl A-C extends, it will be applying force on the B-C axis at 45 deg. This translates into a force of 19550 lbs at point C. This force will then try to rotate the BCD link around point B. As B-D = 2xB-C then force at point D would be 9775. This force is rotational around point B which is, in fact, a floating point moving in an arc from point B to E around point A. As point D raises, due to the floating pivot of point B and the fixed pivot of point H, D will move in a straight line to the fully raised point G. Line D-G is at 90 deg to Line DH therefore there would be 9775 lbs of lift at point D which would diminish as the box raises.
I don't know how to calculate lift force at anywhere higher than the fully down position but in reality, I guess it doesn't matter as the most lift is required at the bottom.
With 19550 of effective force at point C, where does the other 8150 of the 27,700 maximum push from the cyl go?
Spent the afternoon looking at scissor designs and playing with CAD and came up with the following. Please feel free to poke holes in it. This would reuse my existing 4x30 cyl and the existing lower cyl mount.
Point Legend:
A - Existing cyl base mount & scissor base mount
B - Scissor hinge pivot (lowered position)
C - Cyl/scissor mount (lowered position)
D - Scissor/bed mount (lowered position)
E - Scissor hinge pivot (raised position)
F - Cyl/scissor mount (raised position)
G - Scissor/bed mount (raised position)
H - Bed hinge
When the cyl A-C extends, it will be applying force on the B-C axis at 45 deg. This translates into a force of 19550 lbs at point C. This force will then try to rotate the BCD link around point B. As B-D = 2xB-C then force at point D would be 9775. This force is rotational around point B which is, in fact, a floating point moving in an arc from point B to E around point A. As point D raises, due to the floating pivot of point B and the fixed pivot of point H, D will move in a straight line to the fully raised point G. Line D-G is at 90 deg to Line DH therefore there would be 9775 lbs of lift at point D which would diminish as the box raises.
I don't know how to calculate lift force at anywhere higher than the fully down position but in reality, I guess it doesn't matter as the most lift is required at the bottom.
With 19550 of effective force at point C, where does the other 8150 of the 27,700 maximum push from the cyl go?

